
Probleme explicate
Problema Selectiei de Activitati
Enuntul problemei: Ti se dau n activitati impreuna cu timpurile lor de inceput si sfarsit. Presupunand ca o persoana poate lucra doar la o singura activitate la un moment dat, gaseste numarul maxim de activitati pe care le poate efectua intr-un timp minim.
Abordarea solutiei: Deoarece rezolvam aceasta problema folosind o abordare lacoma (greedy), este destul de evident sa alegem o activitate care se termina intr-un timp mai scurt. De ce? Pentru ca astfel vom putea realiza multe sarcini intr-un timp specificat, in loc sa ne concentram doar pe o singura sarcina cu durata mare. Prin urmare, trebuie sa alegem sarcinile in ordine ne-descrescatoare.
Incepe solutia prin sortarea array-urilor date in ordine crescatoare folosind o tehnica de sortare la alegere. Tine cont ca pentru a incepe sa faci activitatile, persoana trebuie sa inceapa cu prima activitate. Asta inseamna ca indiferent de input-urile primite, prima activitate este intotdeauna implementata. De ce? Pentru ca daca faci o singura activitate, nu conteaza care o faci! Tine cont ca persoana va putea sa ia o noua activitate doar dupa ce a terminat activitatea anterioara. Daca persoana este deja ocupata cu activitatea anterioara la acel moment, respinge urmatoarea activitate si continua. Asadar, selecteaza activitatea urmatoare daca timpul de start al acesteia este mai mare sau egal cu timpul de sfarsit al activitatii anterioare. Exemplu:
Input: start[]={10,12,20} ; finish[]={20,25,30}
Output: {10,20}, {20,30}
Explicatie: Am inteles deja ca prima sarcina este implementata oricum. Deci, se adauga sarcina {0} in array-ul solutiei. Continuand, timpul de sfarsit al primei sarcini este comparat cu timpul de start al sarcinii {1}. Deoarece este mai mic decat timpul de sfarsit al activitatii anterioare, trecem mai departe. Comparatia se repeta si sarcina {2} este selectata.
Problema in c++:
#include <bits/stdc++.h>
using namespace std;
int main() {
// Implementarea array-ului pentru prețurile acțiunilor pe zilele i
int n = 6;
vector<int> prices = {7,1,5,3,6,4};
// Pentru a stoca cele mai bune zile pentru cumpărare și vânzare de acțiuni
pair<int,int> ans;
// Pentru a stoca profitul maxim
int maxProfit = 0;
// Pentru a stoca cumpărarea minimă de acțiuni
int minBuy = INT_MAX;
// Indexul pentru minBuy
int ind;
for(int i = 0; i < prices.size(); i++) {
// Dacă găsim un preț minim de cumpărare mai mic decât cel anterior, actualizăm minBuy și indicele său
if(minBuy > prices[i]) {
ind = i;
minBuy = prices[i];
}
// Găsirea profitului maxim prin verificarea vânzării acțiunilor în ziua i la prețul minBuy
if(maxProfit < prices[i] - minBuy) {
maxProfit = prices[i] - minBuy;
ans = {ind, i}; // stocarea zilelor de cumpărare și vânzare
}
}
// Afișarea celei mai bune zile pentru cumpărare și vânzare de acțiuni și a profitului maxim
cout << "Cea mai bună zi pentru cumpărare este ziua " << ans.first + 1 << " și cea mai bună zi pentru vânzare este ziua " << ans.second + 1 << endl;
cout << "Profitul maxim va fi " << maxProfit;
return 0;
}
Problemă: Cea mai bună zi pentru a cumpăra și vinde acțiuni
Enunțul problemei: Vi se dă un vector prices[] care conține prețul unei acțiuni în unele zile. Trebuie să alegeți o zi pentru a cumpăra acțiunile și o altă zi pentru a le vinde. Returnați zilele în care cumpărați și vindeți acțiunile. Abordare pentru rezolvare: În această problemă, nu aveți nevoie să știți nimic despre acțiuni, abordarea pe care o oferim este suficient de simplă pentru a fi înțeleasă chiar și de începători. Acum, este destul de evident că atunci când doriți să cumpărați ceva, doriți să plătiți cel mai mic preț posibil. Similar, atunci când vindeți același lucru, doriți să vă creșteți profiturile prin vânzarea la un preț mai mare. Deci, sunteți avid să vă măriți profiturile. Așadar, să vedem cum veți proceda în această problemă:
Aici, sortarea nu va funcționa deoarece trebuie să oferiți numărul zilei. Așadar, veți găsi mai întâi valoarea minimă a acțiunilor din prices[]. Indexul valorii minime va deveni ziua în care cumpărați acțiunile. Pentru a vinde acțiunile, trebuie să verificați valoarea acțiunilor în zilele după ce ați cumpărat acțiunile. Așadar, rulați un bucluc până la sfârșit, începând de la ziua de cumpărare și găsiți valoarea maximă a acțiunilor în vectorul rămas. Acum, scădeți valoarea zilei de cumpărare de la ziua de vânzare și gata! Ați obținut răspunsul! Exemplu:
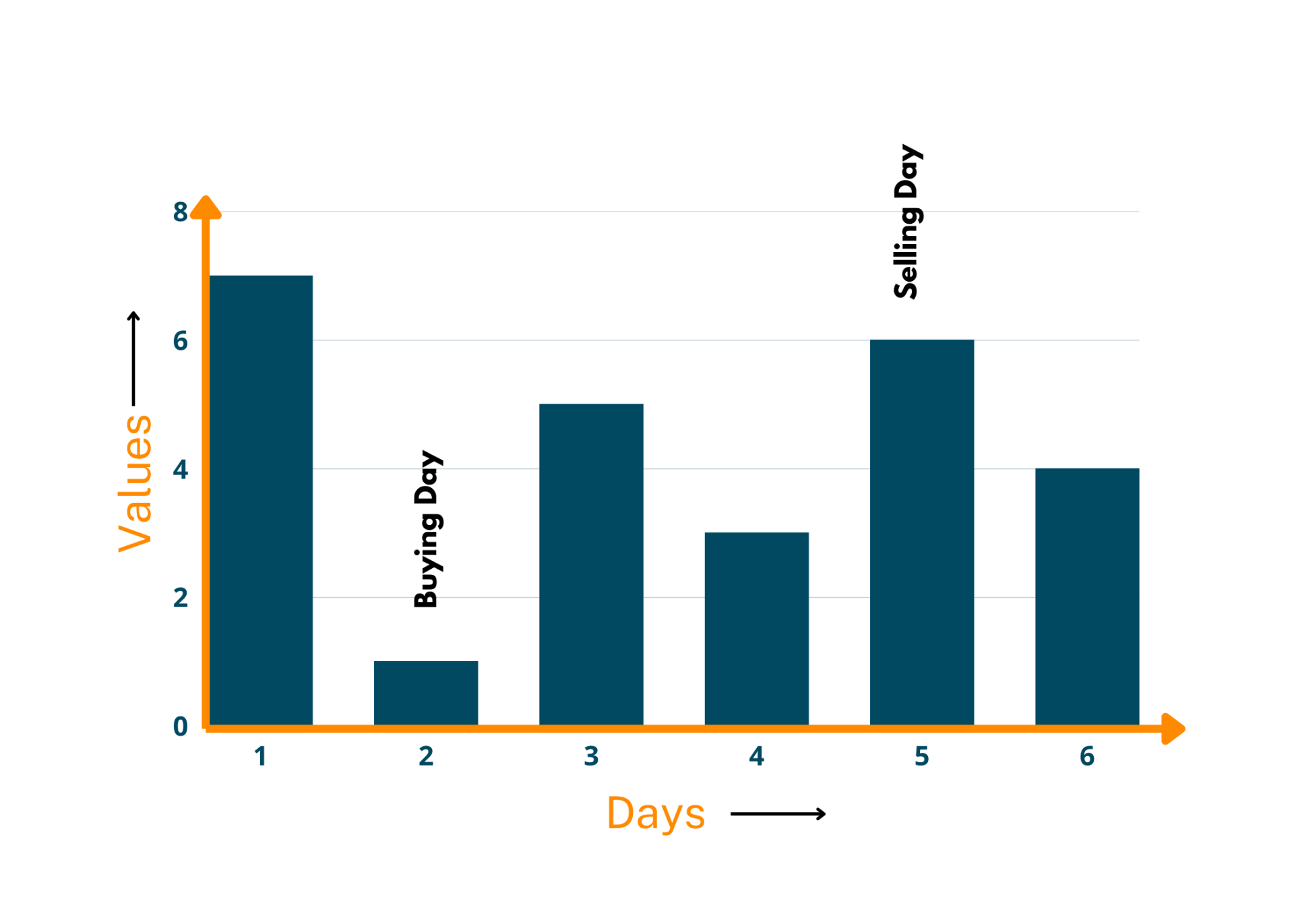
Input: {7,1,5,3,6,4}
Output: 5
Explicație: După cum am menționat în abordare, mai întâi veți găsi elementul cel mai mic, care este 1, în acest caz. Acum, ziua de cumpărare devine 1. După aceea, căutăm valoarea maximă a acțiunilor în zilele care urmează după 1. Așadar, ziua de vânzare devine ziua în care acțiunile au valoarea 6. Acum, calculăm diferența dintre cele două zile și obținem 5 ca rezultat. Uitați-vă la ilustrația de mai jos.
Numărul minim de monede
Enunțul problemei: Avem o valoare V și trebuie să dăm restul în monede indiene. Acum, denominațiile monedelor sunt 1, 2, 5, 10, 20, 50, 100, 200, 500, 2000. Rezultatul ar trebui să conțină cel mai mic număr posibil de monede pentru valoarea dată.
Abordarea către soluție: Din nou, deoarece trebuie să găsim cel mai mic număr posibil de monede în schimbul valorii V, vom folosi o abordare greedy (lacomă). Deci, vom începe cu moneda cu cea mai mare valoare care este mai mică sau egală cu V. Apoi vom scădea valoarea monedei alese din valoarea dată. Pentru valoarea rămasă, vom căuta din nou moneda cu cea mai mare valoare și o vom adăuga la răspuns. Urmați pașii de mai jos:
- Găsiți moneda cu cea mai mare valoare dintre cele date.
- Adăugați-o la rezultat și scădeți-o din V.
- Repetați pașii de mai sus până când găsiți valoarea completă.
Exemplu:
Input: V=70
Output: 2
Explicație: Pentru a da restul de 70, vom avea nevoie de o bancnotă de 50 și încă una de 20.


Conectarea a 'n' frânghii cu cost minim
Enunțul problemei: Aveți n frânghii de lungimi diferite. Acum, trebuie să conectați aceste frânghii într-una singură. Găsiți costul minim al unirii tuturor frâghiilor într-una singură. Se presupune că costul de unire a frâghiilor este egal cu suma lungimilor lor.
Abordarea către soluție: Ideea din spatele acestei probleme este să adăugăm întâi cele două frânghii ale căror costuri de unire sunt minime. Apoi, vom uni din nou cele două frânghii ale căror costuri de unire sunt cele mai mici. La fel, vom itera prin toate frânghiile. Pentru aceasta, vom folosi o min-heap într-o coadă de prioritate (priority queue). Urmați pașii de mai jos:
- Utilizați o min-heap într-o coadă de prioritate.
- Luați primele 2 elemente (cele mai mici) și le adăugați. Suma va fi adăugată la rezultat.
- Acum, vă rămâne cu un element mai puțin. Aplicați aceeași abordare.
- Continuați să faceți aceste pași până când obțineți un singur răspuns.
Exemplu:
Input: {5,4,2,8}
Output: 36
Explicație: În primul rând, inițializați o variabilă numită Result=0. Nu uitați să adăugați costul de unire a frânghiilor la această variabilă. Acum, vom conecta frâghiile de lungimi 4 și 2. Astfel, Result=6. Acum, ne-au rămas frânghii {5,6,8}. Apoi, vom lua din nou cele 2 elemente minime din vector și le vom adăuga. Result=6+11. Acum, vom uni elementele rămase care sunt 11 și 8. Astfel, în final, Result=6+11+19. Prin urmare, rezultatul final este 36.Pentru o înțelegere mai simplă, observați ilustrația de mai jos.



